End-to-End Learning of Coherent Probabilistic Forecasts for Hierarchical Time Series-论文阅读

ICML 2021：时间序列
论文： 层级时间序列相关概率预测端到端学习方法

论文地址：http://proceedings.mlr.press/v139/rangapuram21a/rangapuram21a.pdf
论文代码：https://github.com/rshyamsundar/gluonts-hierarchical-ICML-2021

主要内容

本文提出了一种分层时间序列预测的新方法，该方法无需任何明确的后处理协调即可产生连贯的概率预测。与最先进的方法不同，所提出的方法同时从层次结构中的所有时间序列中学习，
并将协调步骤合并到一个可训练的模型中。这是通过应用重新参数化技巧并将协调转换为具有封闭形式解决方案的优化问题来实现的。这些模型特征使分层预测的端到端学习成为可能，
同时完成生成概率性和连贯性预测的挑战性任务。重要的是，我们的方法还适应一般聚合约束，包括分组和时间层次结构。对现实世界分层数据集的广泛实证评估证明了所提出的方法相对于最先进的方法的优势。

模型介绍

现有层次预测存在问题：

1. 每个时间序列的模型参数独立学习，从而丢弃中间过程信息
2. 大多数现有方法只能产生点的预测，而不是概率性的预测

提出新的层次预测：

1. 结合学习和和解到一个单一的端到端模型。模型参数可以同时从层次结构中的所有时间序列中学习出来。从模型的概率预测保证是一致的，而不需要任何后处理步骤
2. 点预测只告诉期望是多少没有置信区间，但是概率预测两者都有，给出期望和波动（置信区间）

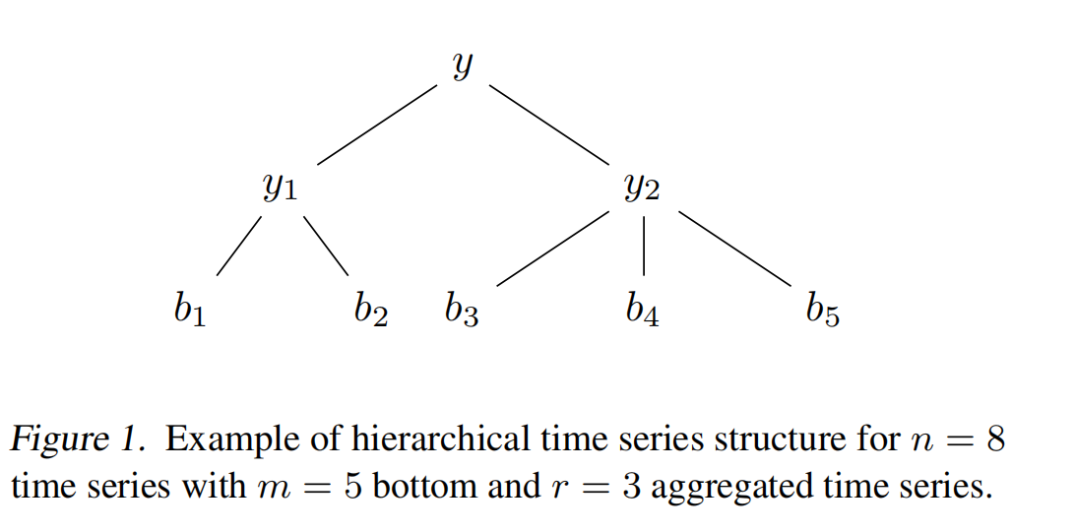
   yt 是采样的矩阵， A 是 y的0空间矩阵；0空间矩阵有很多，找出一个 y 使得 它离 Yt 最近的矩阵 其中AY = 0; 保证层次预测中，底部和相加等于顶部；  

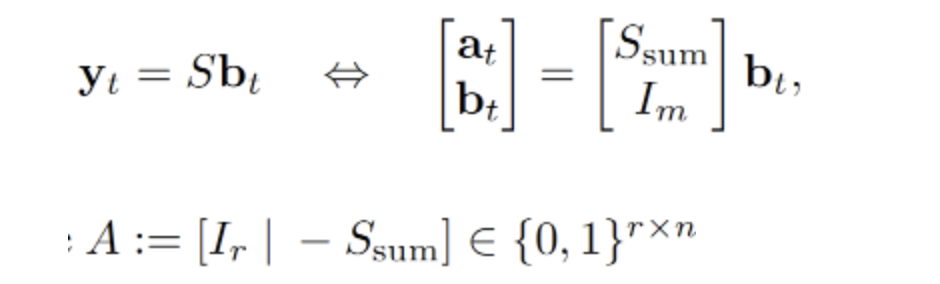
计算M矩阵，最小二乘法线性回归的求解过程 ，其中I 是 对角线上的元素为 1，其他位置的元素为 0 的单位矩阵；

模型架构

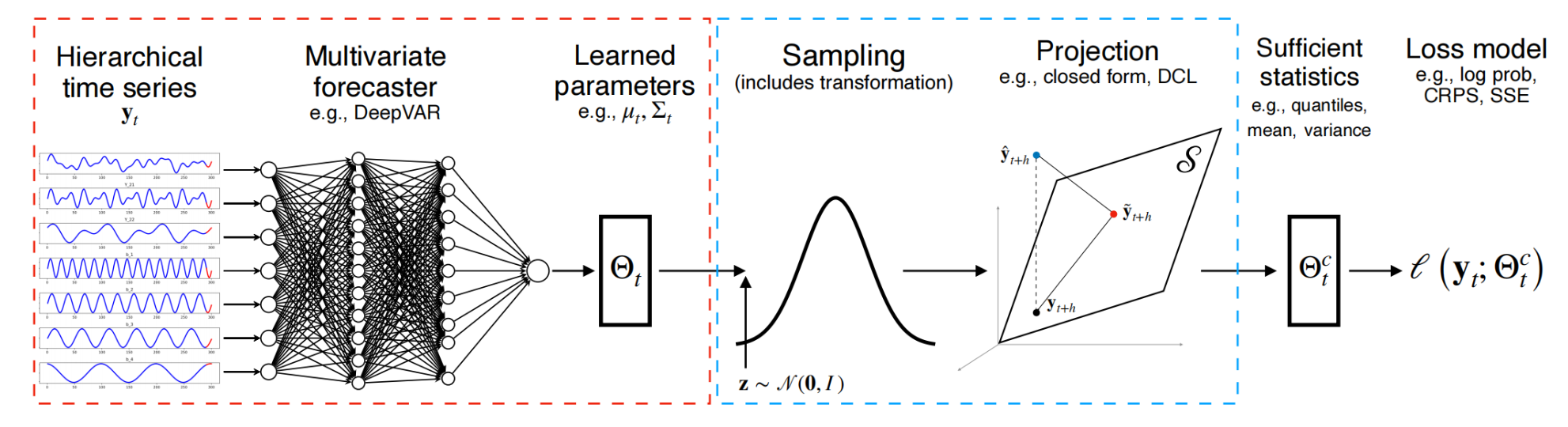
层次时间序列数据用于训练一个多元预测者。学习到的分布参数以及重新参数化技巧允许在训练期间对该分布进行采样。可选择地，对样本的非线性变换(e。g., 标准化流)可以解释非高斯域内的数据。

端到端层次结构预测

一个预测模型，在预测范围上产生多元预测分布 采样和投影步骤，从预测分布中抽取样本，然后投影到相干子空间上

deepVar作为基础baseline多元预测

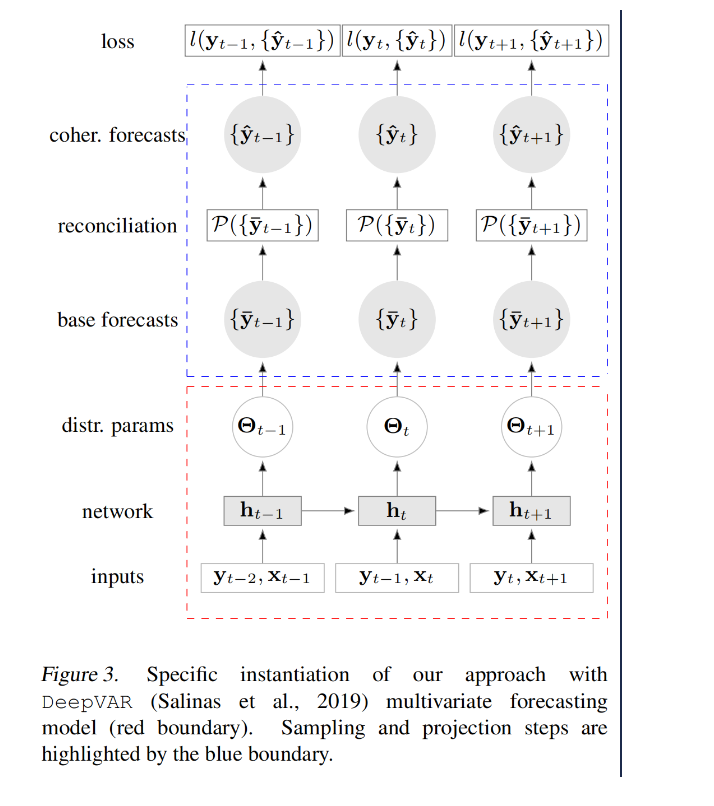
网络结构

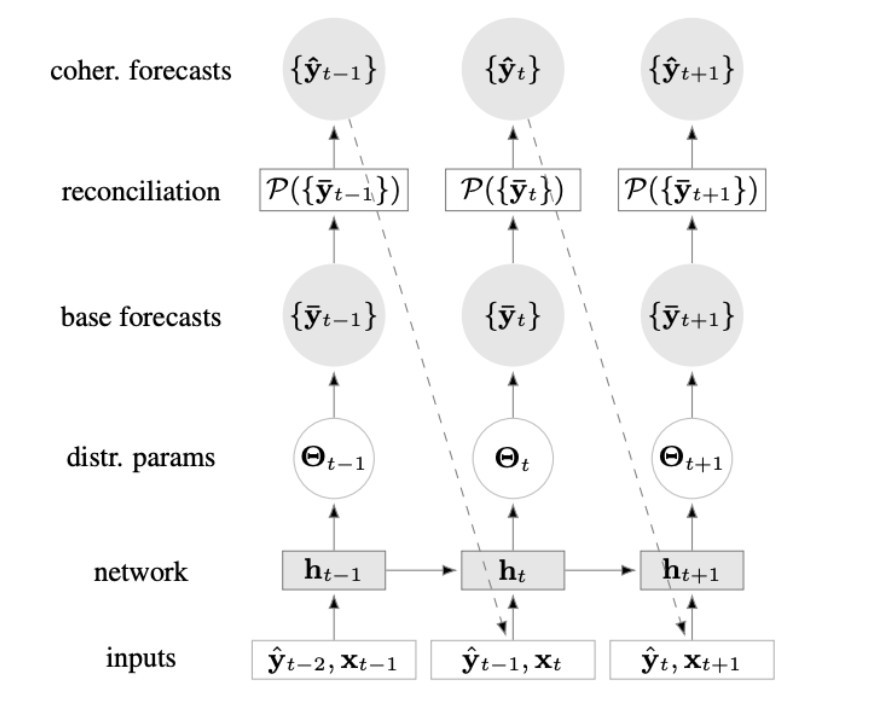
采样和投影

1. 采样

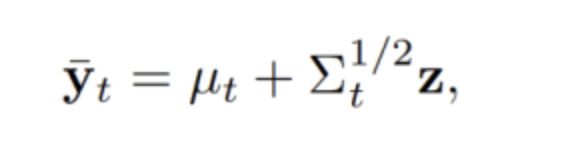
参数映射到N(0, I) 空间，采样一部分数据

1. 投影

通过投影，把预测问题转成优化问题

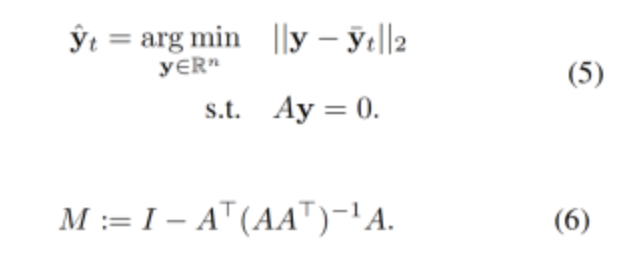
模型代码：https://github.com/rshyamsundar/gluonts-hierarchical-ICML-2021/blob/master/src/gluonts/model/deephier/_network.py

输入参数：

1. F：表示深度学习框架MXNet张量
2. target_dimension_indicator：目标维度的索引（批大小，目标维度）
3. past_time_feat：过去时间序列的动态特征（批大小，历史长度，特征数）
4. past_target_cdf：过去目标值的边际CDF转换结果（批大小，历史长度，目标维度）
5. past_observed_values：指示值是否被观察到的指示器（批大小，历史长度，目标维度）
6. past_is_pad：指示过去目标值是否已填充的指示器（批大小，历史长度）
7. future_time_feat：未来时间特征（批大小，预测长度，特征数）
8. future_target_cdf：未来目标值的边际CDF转换结果（批大小，预测长度，目标维度）
9. future_observed_values：指示未来值是否被观察到的指示器（批大小，预测长度，目标维度）
10. epoch_frac：表示当前epoch的分数值

    输出：

11. distr：形状为（批大小，1）的损失
12. likelihoods：每个时间步的似然值（批大小，上下文长度+预测长度，1）
13. distr_args：分布参数（上下文长度+预测长度，参数数量）

    执行步骤：

14. 计算序列长度（seq_len），即上下文长度和预测长度之和。
15. 使用unroll_encoder方法展开编码器，得到rnn_outputs、scale、lags_scaled和inputs。
16. 将过去和未来的目标CDF值连接起来形成目标序列。
17. 使用distr方法构建分布（distr）及其参数（distr_args）。
18. 检查CRPS权重、似然权重和与采样相关的参数的有效性。
19. 如果CRPS权重大于零或启用了采样，则从多元高斯分布中进行采样。
20. 计算使用采样值或网络参数得到的预测值的似然值。
21. 根据观测到的值，使用CRPS损失、似然值和权重计算损失。
22. 将损失、似然值和分布参数作为输出返回。

实验评估

评价CRPS: 评估预测分布的准确性，类似于MAE, 越小越好 </br>

1. 连续分级概率评分（Continuous Ranked Probability Score, CRPS）或“连续概率排位分数”是一个函数或统计量，可以量化一个连续概率分布（理论值）与确定性观测样本（真实值）间的差异；
2. CRPS在数学形式上是累积分布函数与阶跃函数（Heaviside step function）之差的平方在实数域的积分，因此可视为平均绝对误差（Mean Absolute Error, MAE）在连续概率分布上的推广。

初步评估

运行5次，算出CRPS分数的平均值和标准差，取最好的结果

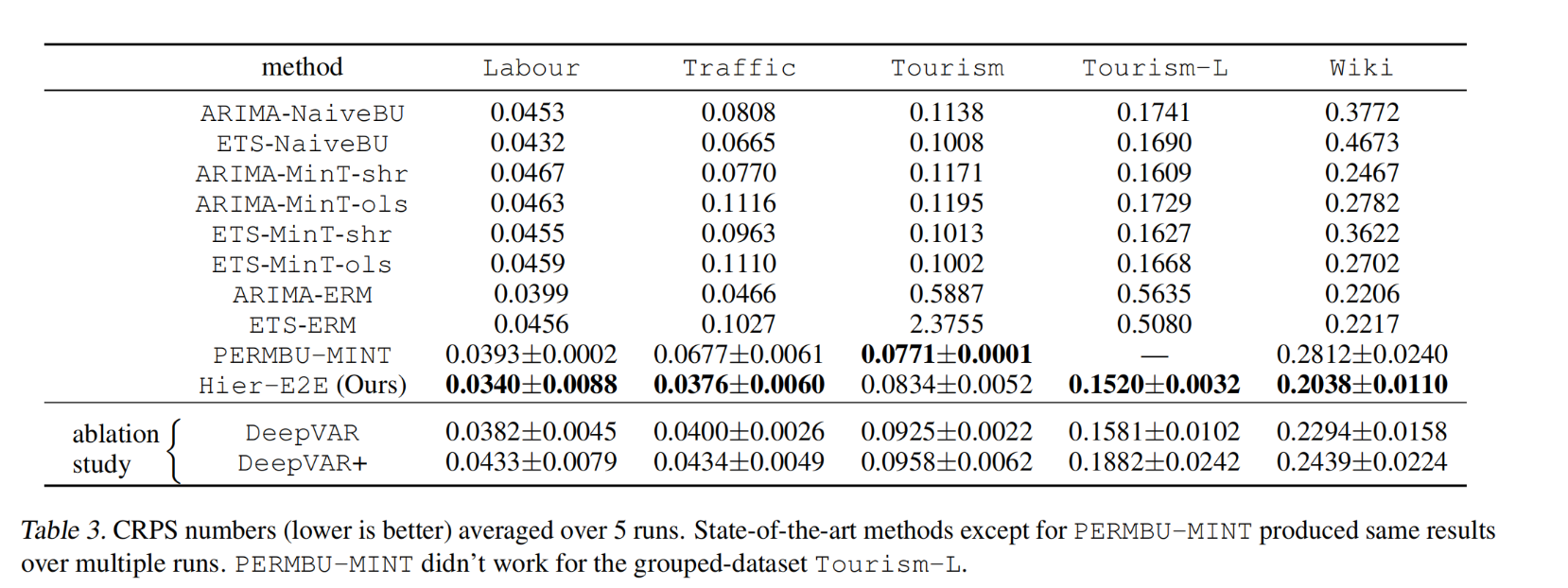
进一步评估

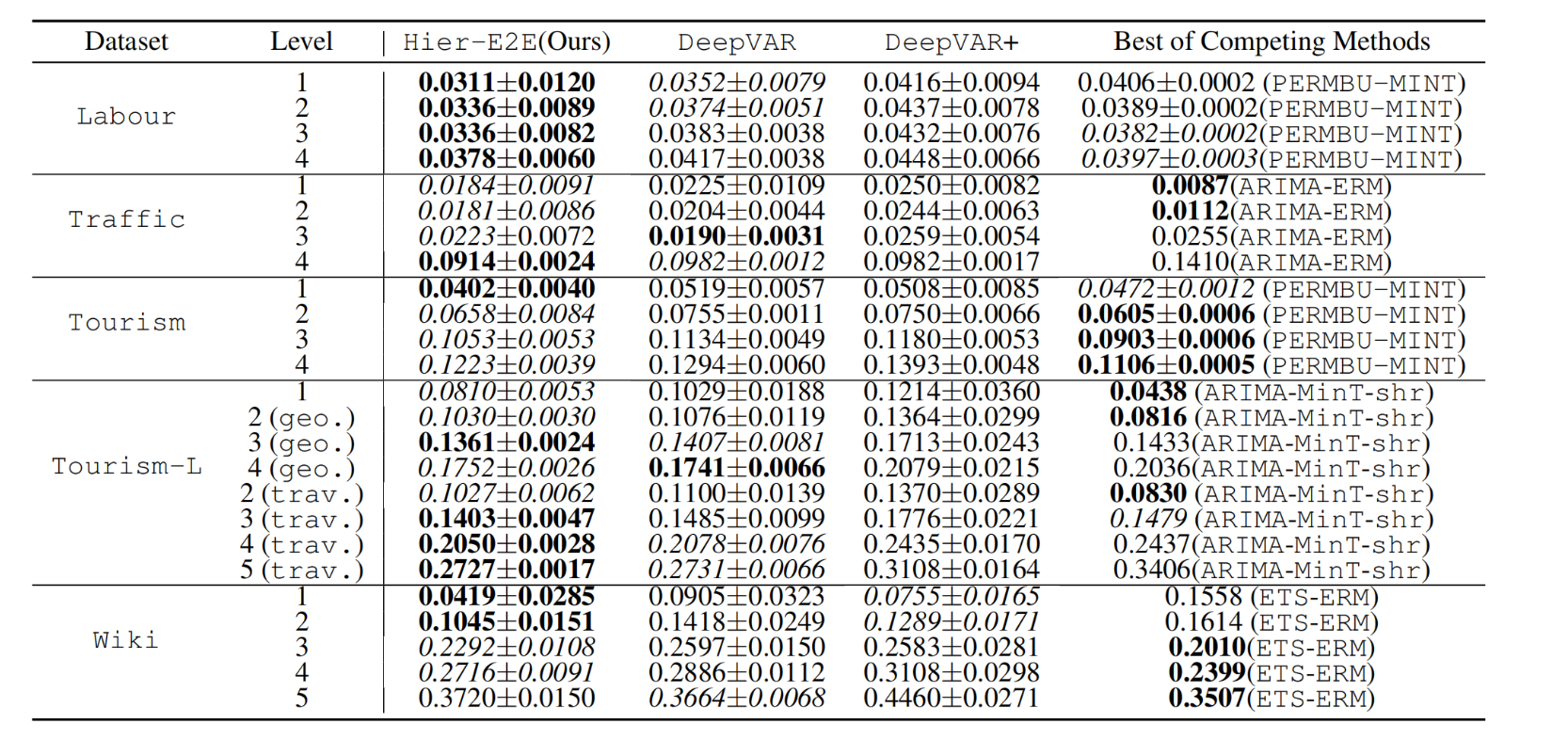
在每个聚合级别上计算的时间序列的平均CRPS分数（越低越好），平均超过5次运行。
这里我们只包括性能最好的竞争方法的结果以及我们的方法及其变体。对于每个数据集，我们选择了在尽可能多的聚合级别中获得最佳结果的竞争方法。
在联系的情况下，选择获得最佳总体CRPS得分的方法（在层次结构中所有级别的平均）

结论

我们提出了一种新的层次时间序列的概率预测方法。主要的新颖之处在于提出了一个单一的global模型，它不需要任何调整来产生连贯的概率预测，这是同类模型中的第一次。此外，该方法可以很容易地处理更一般的结构约束，超越了层次设置的可微凸优化层我们的方法是通用的，因为我们可以将它添加到大多数现有的深度预测模型中。我们的经验表明，训练一个单一的、全局的模型和执行一致性，比之前的最先进的使用两步程序而不是端到端学习获得更好的结果。虽然我们从经验上发现，多元高斯分布在所考虑的数据集上表现良好，但作为未来的工作，我们希望探索使用非线性变换，如归一化流来更好地建模非高斯数据。                                                                                                                                                                                                                                                    

优缺点

优点

可校验性高：总值拆分可以根据和值来校验是否一致，很容易判断合理性。

参数共享：它能在时间步上共享相同的参数，这使得模型具有较少的参数量。参数共享使得模型更加高效，尤其是对于长序列数据。

缺点        

计算效率较低：使用deepVAR作为基础结构，实际上就是RNN网络，计算过程是顺序的，每个时间步的计算需要等待前一个时间步的结果。这限制了并行计算的能力，导致训练速度较慢。 模型结构复杂：网络模型结构复杂，预测流程过长；如果中间某个环节出现问题，对端到端预测影响巨大。